Language of models



ENST/MRNE 222 Environmental Data Analysis and Visualization

What is a model?

Statistical modelling

  • We use models to explain the relationship between variables and to make predictions
  • For now we will focus on linear models (but there are many other types of models too)

Data: Paris Paintings

Paris Paintings

pp <- read_csv("data/paris-paintings.csv", na = c("n/a", "", "NA")) |> 
  clean_names()
  • Source: Printed catalogs of 28 auction sales in Paris, 1764 - 1780
  • Data curators Sandra van Ginhoven and Hilary Coe Cronheim (who were PhD students in the Duke Art, Law, and Markets Initiative at the time of putting together this dataset) translated and tabulated the catalogs
  • 3393 paintings, their prices, and descriptive details from sales catalogs over 60 variables

Paris Paintings

names(pp)
 [1] "name"              "sale"              "lot"              
 [4] "position"          "dealer"            "year"             
 [7] "origin_author"     "origin_cat"        "school_pntg"      
[10] "diff_origin"       "logprice"          "price"            
[13] "count"             "subject"           "authorstandard"   
[16] "artistliving"      "authorstyle"       "author"           
[19] "winningbidder"     "winningbiddertype" "endbuyer"         
[22] "interm"            "type_intermed"     "height_in"        
[25] "width_in"          "surface_rect"      "diam_in"          
[28] "surface_rnd"       "shape"             "surface"          
[31] "material"          "mat"               "material_cat"     
[34] "quantity"          "nfigures"          "engraved"         
[37] "original"          "prevcoll"          "othartist"        
[40] "paired"            "figures"           "finished"         
[43] "lrgfont"           "relig"             "lands_all"        
[46] "lands_sc"          "lands_elem"        "lands_figs"       
[49] "lands_ment"        "arch"              "mytho"            
[52] "peasant"           "othgenre"          "singlefig"        
[55] "portrait"          "still_life"        "discauth"         
[58] "history"           "allegory"          "pastorale"        
[61] "other"

Paris art auction

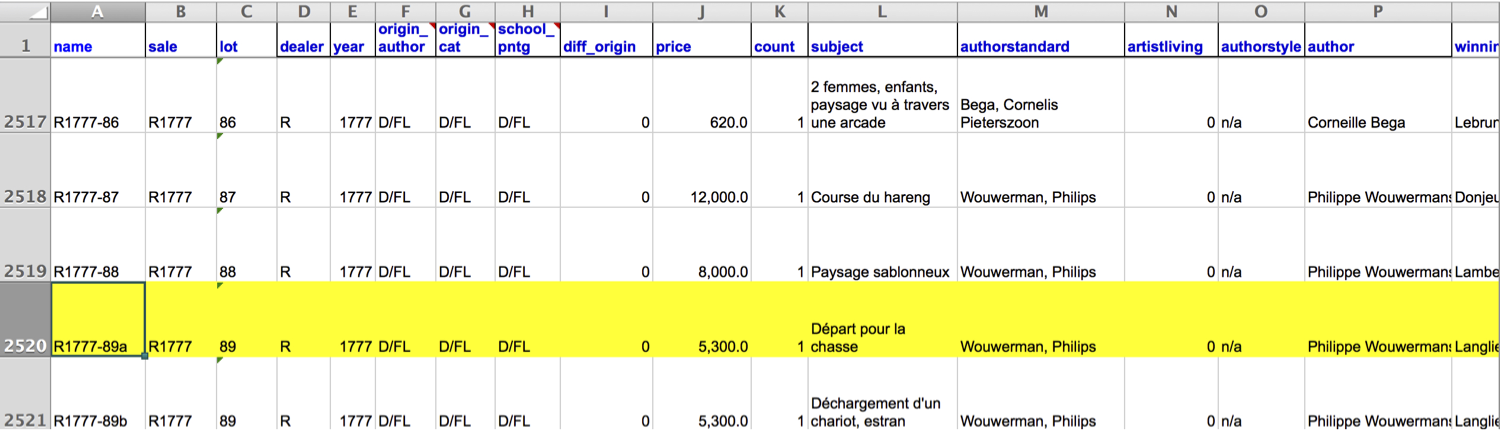
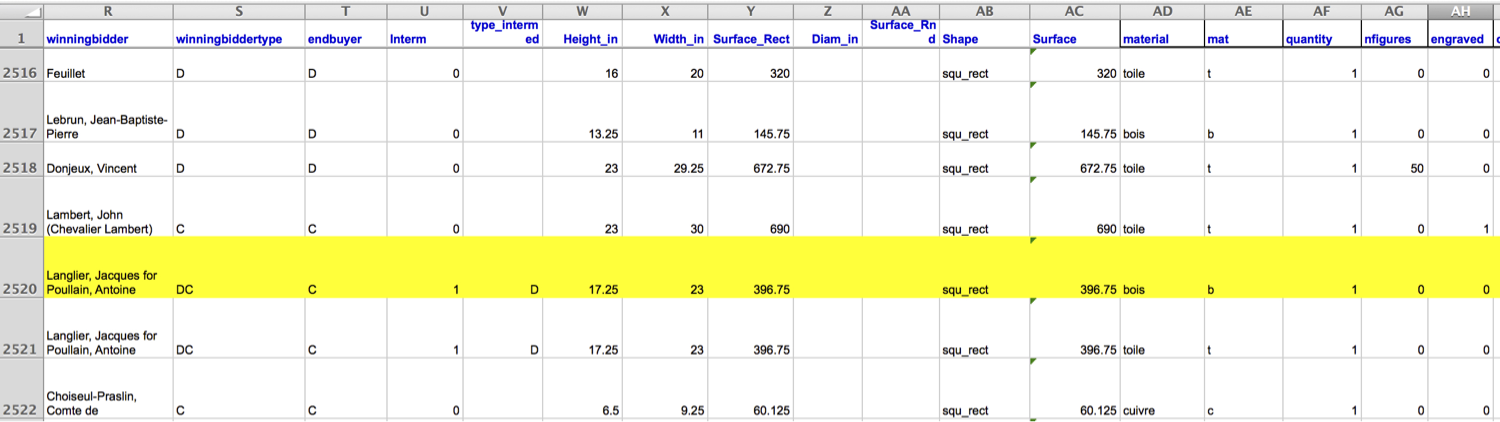
Data was scraped from auction catalog text

“Two paintings very rich in composition, of a beautiful execution, and whose merit is very remarkable, each 17 inches 3 lines high, 23 inches wide; the first, painted on wood, comes from the Cabinet of Madame la Comtesse de Verrue; it represents a departure for the hunt: it shows in the front a child on a white horse, a man who gives the horn to gather the dogs, a falconer and other figures nicely distributed across the width of the painting; two horses drinking from a fountain; on the right in the corner a lovely country house topped by a terrace, on which people are at the table, others who play instruments; trees and fabriques pleasantly enrich the background.”

Dataset contains numeric and categorical variables

Modeling the relationship between variables

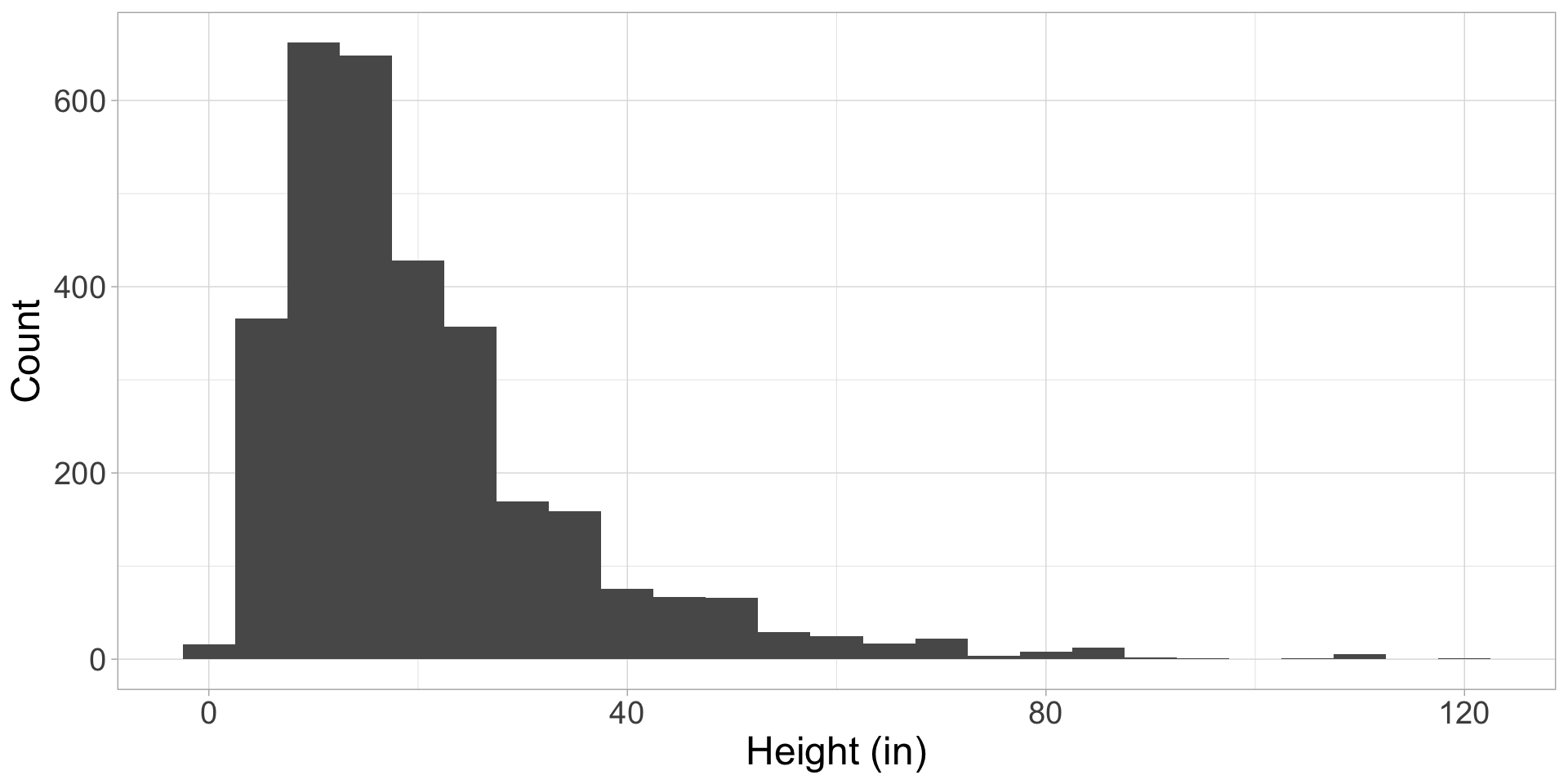
Heights

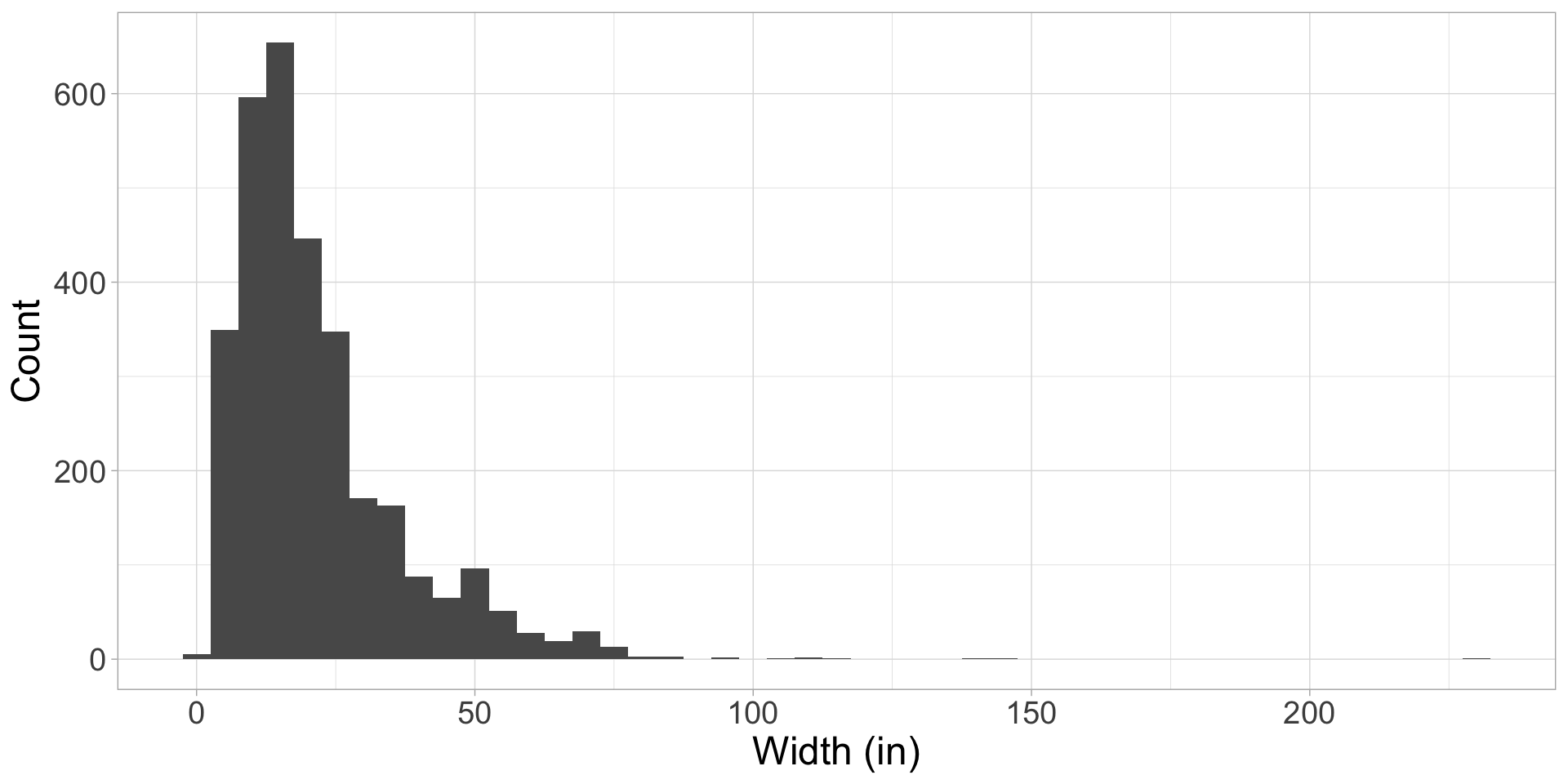
Widths

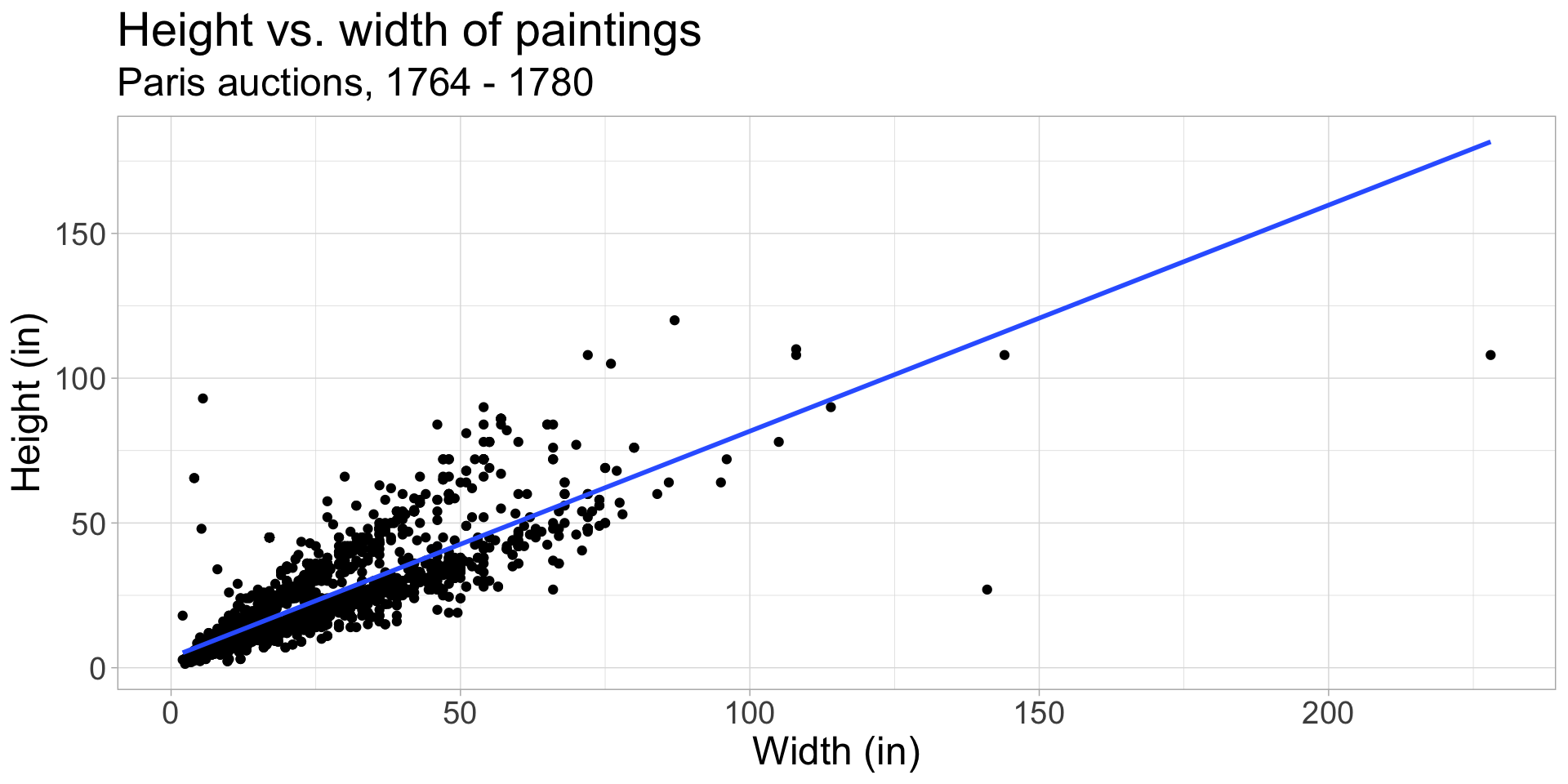
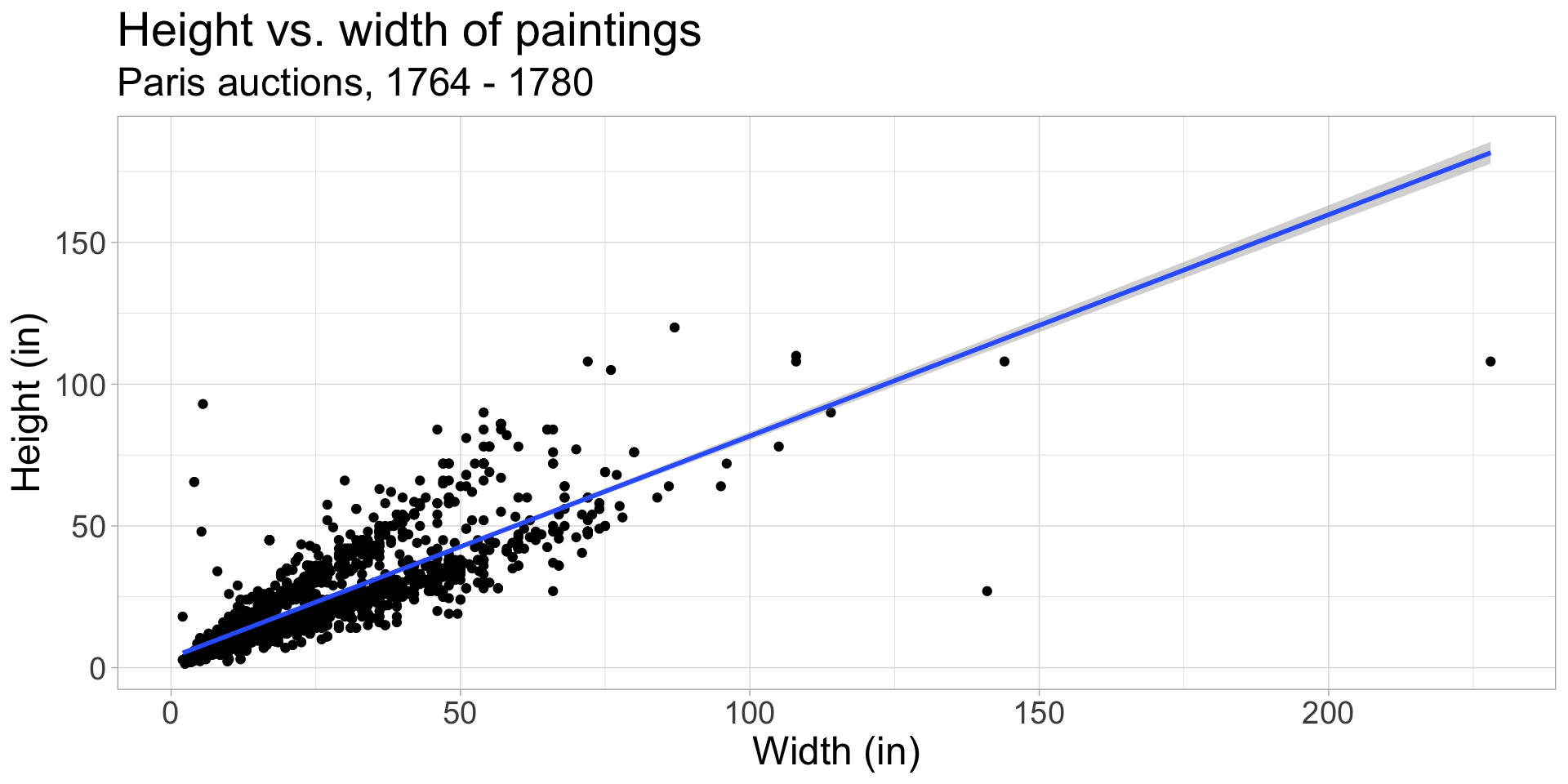
Height vs. width

As width increases, height increases:

Models as functions

  • We can represent relationships between variables using functions
  • A function is a mathematical concept: it describes the relationship between an output and one or more inputs
    • If you know the inputs, you can use them to calculate the output
    • Example: The formula \(y = 3x + 7\) is a function with input \(x\) and output \(y\). If \(x\) is \(5\), \(y\) is \(22\), \(y = 3 \times 5 + 7 = 22\)
    • This function should be familiar? It describes the equation of a line.

Height as a function of width

If we know a painting’s width, we can use the equation of the line to calculate the expected height value for a given width.

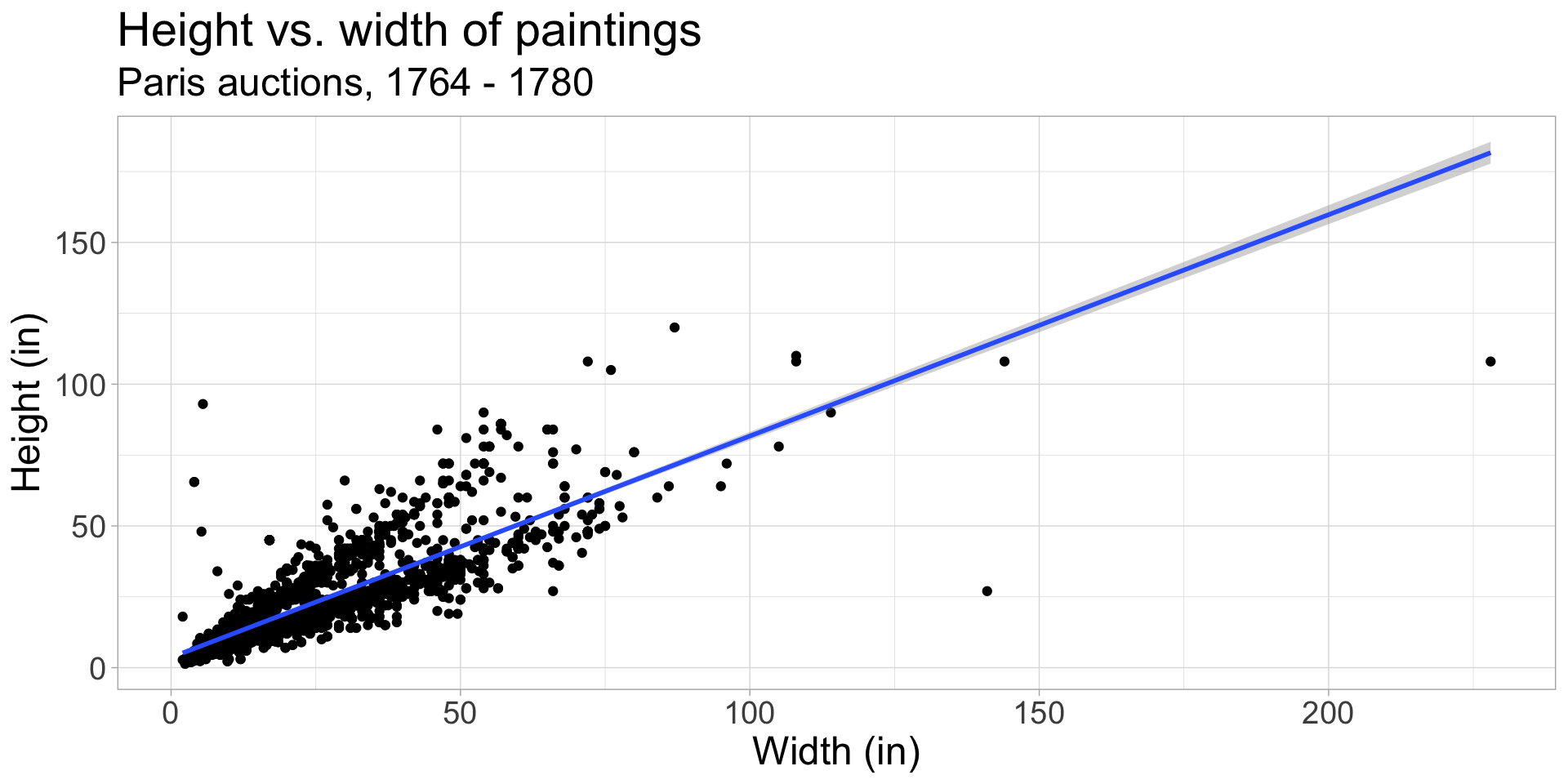
Use geom_smooth(method = "lm") to draw a straight line through your data

ggplot(data = pp, aes(x = width_in, y = height_in)) +
  geom_point() +
  geom_smooth(method = "lm") +
  labs(
    title = "Height vs. width of paintings",
    subtitle = "Paris auctions, 1764 - 1780",
    x = "Width (in)",
    y = "Height (in)"
  )

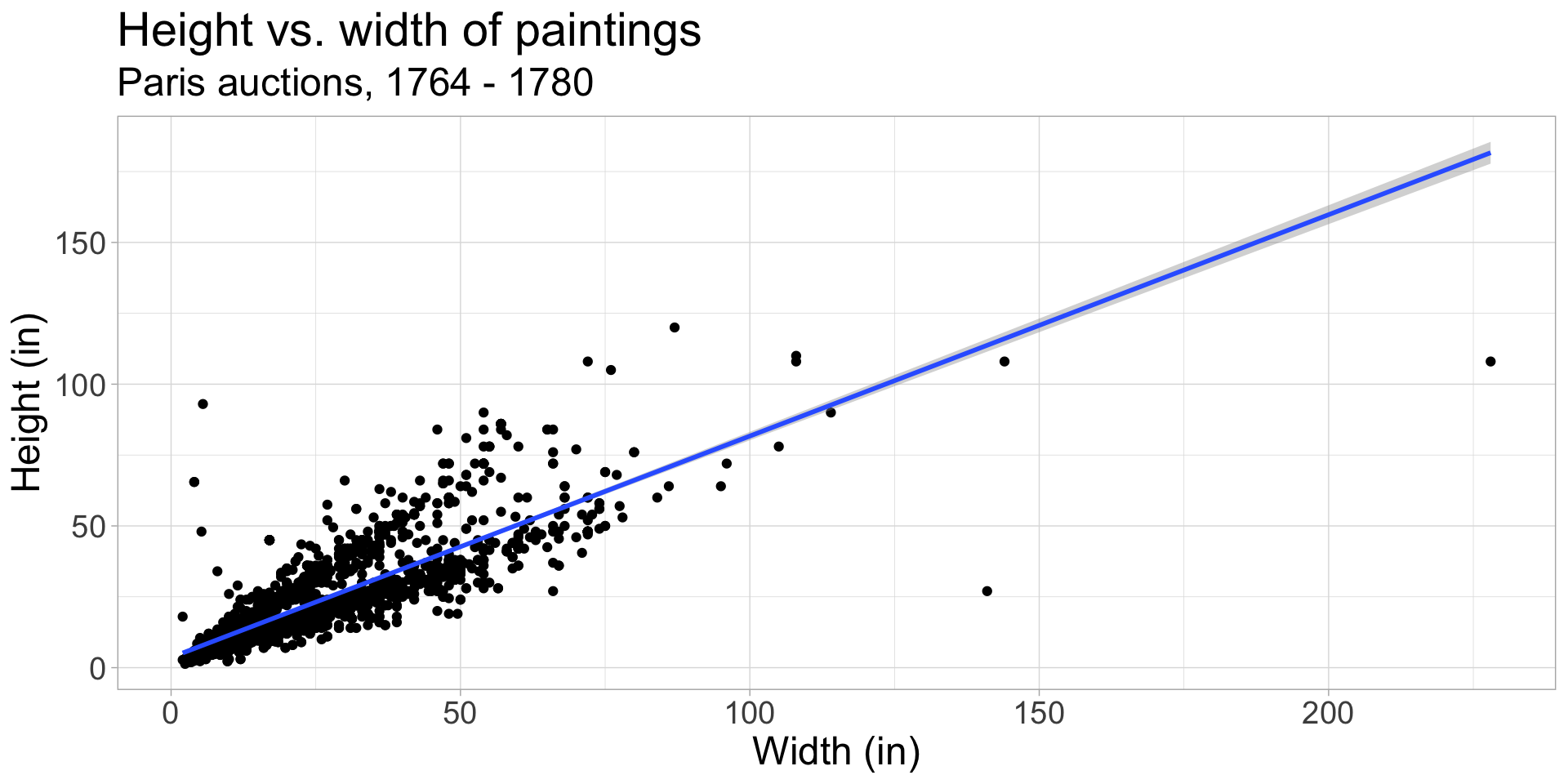
  • The gray shading above and below the line represent the confidence interval (CI): the range of values within which the predicted values of y (height) are expected to lie.
  • by default, geom_smooth() uses a 95% CI: 95% percent chance that the actual height is within the range of predicted values in the interval

Use geom_smooth(method = "lm", se = FALSE) to remove the CI from the plot

ggplot(data = pp, aes(x = width_in, y = height_in)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) +
  labs(
    title = "Height vs. width of paintings",
    subtitle = "Paris auctions, 1764 - 1780",
    x = "Width (in)",
    y = "Height (in)"
  )

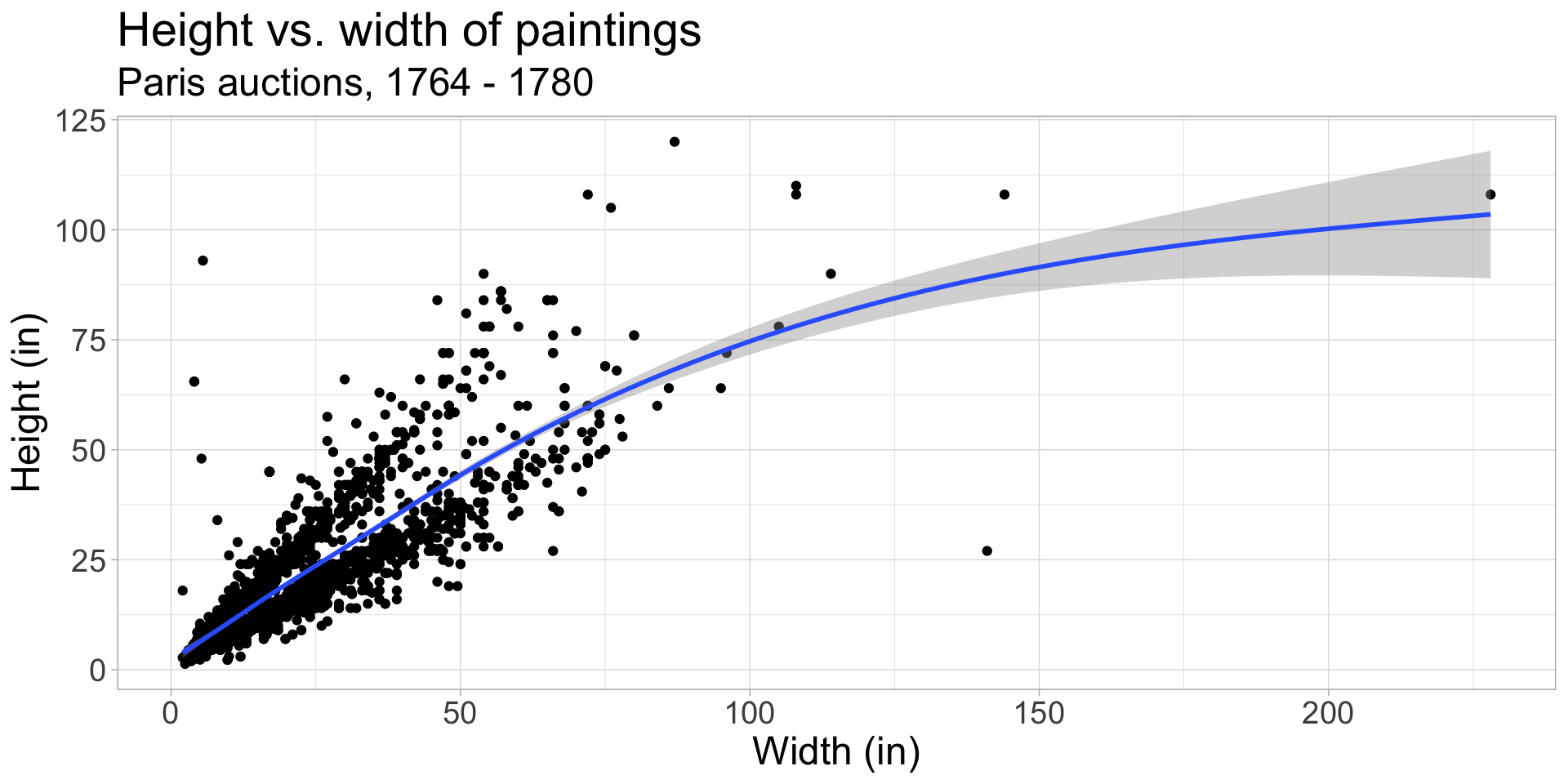
Other smoothing methods: gam

Fits line using a generalized additive model (GAM): allows for non-linear relationships using smoothing functions

ggplot(data = pp, aes(x = width_in, y = height_in)) +
  geom_point() +
  geom_smooth(method = "gam") +
  labs(
    title = "Height vs. width of paintings",
    subtitle = "Paris auctions, 1764 - 1780",
    x = "Width (in)",
    y = "Height (in)"
  )

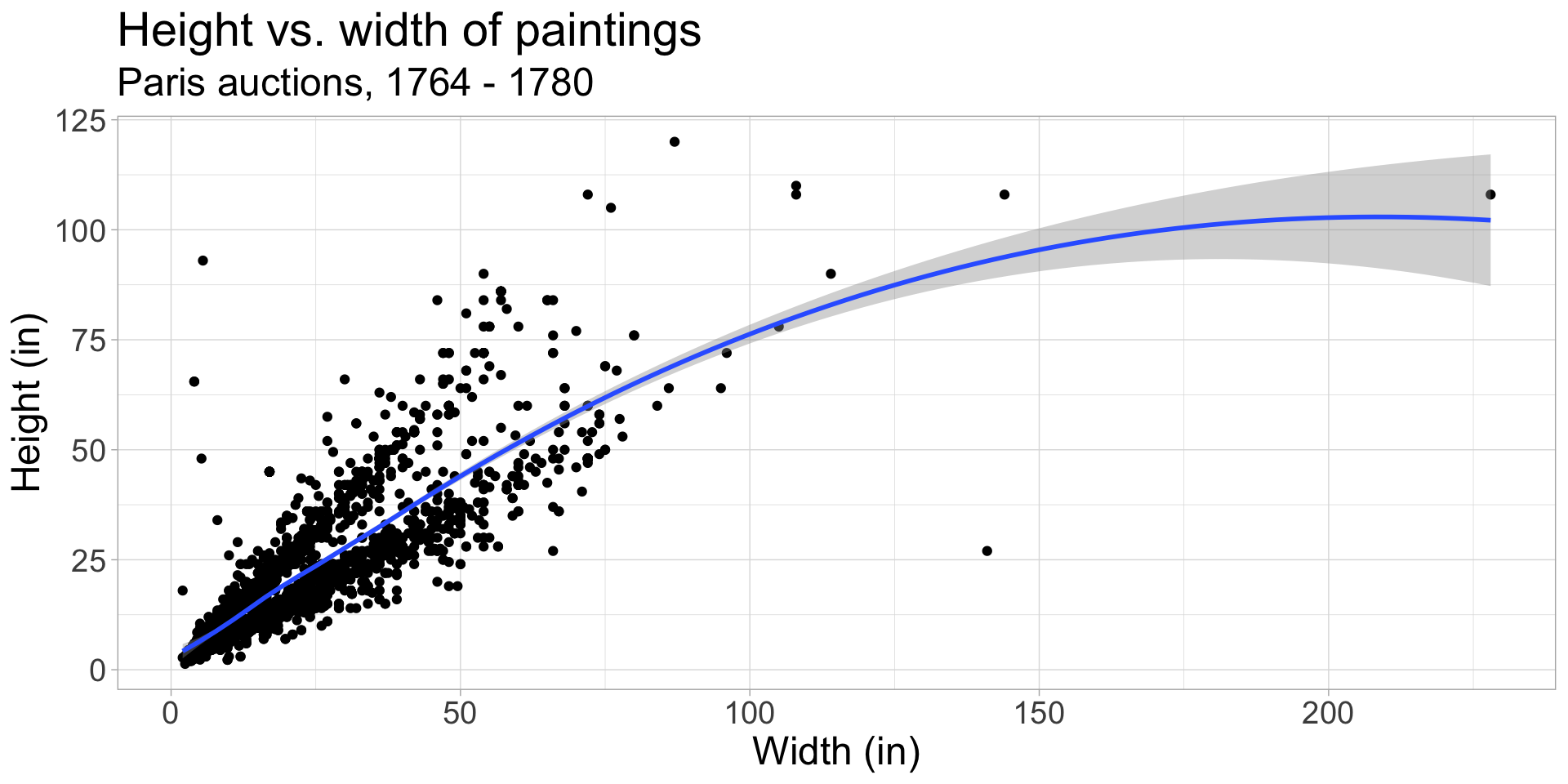
Other smoothing methods: loess

Locally estimated scatterplot smoothing (loess): another method that allows for non-linear relationships

ggplot(data = pp, aes(x = width_in, y = height_in)) +
  geom_point() +
  geom_smooth(method = "loess") +
  labs(
    title = "Height vs. width of paintings",
    subtitle = "Paris auctions, 1764 - 1780",
    x = "Width (in)",
    y = "Height (in)"
  )

Model vocabulary

  • Response variable: Variable whose behavior or variation you are trying to understand; plotted on the y-axis. Also called the dependent variable.

  • Explanatory variables: Other variable(s) used to explain the variation in the response; plotted on the x-axis. Also called independent or predictor variables.

  • Predicted value: Output of the model function

    • The model function gives the typical (expected) value of the response variable conditioning on the explanatory variables

  • Residuals: A measure of how far each observed value is from its predicted value (based on a particular model)

    • Residual = Observed value - Predicted value
    • Tells how far above/below the expected value each observation is

Residuals visualized

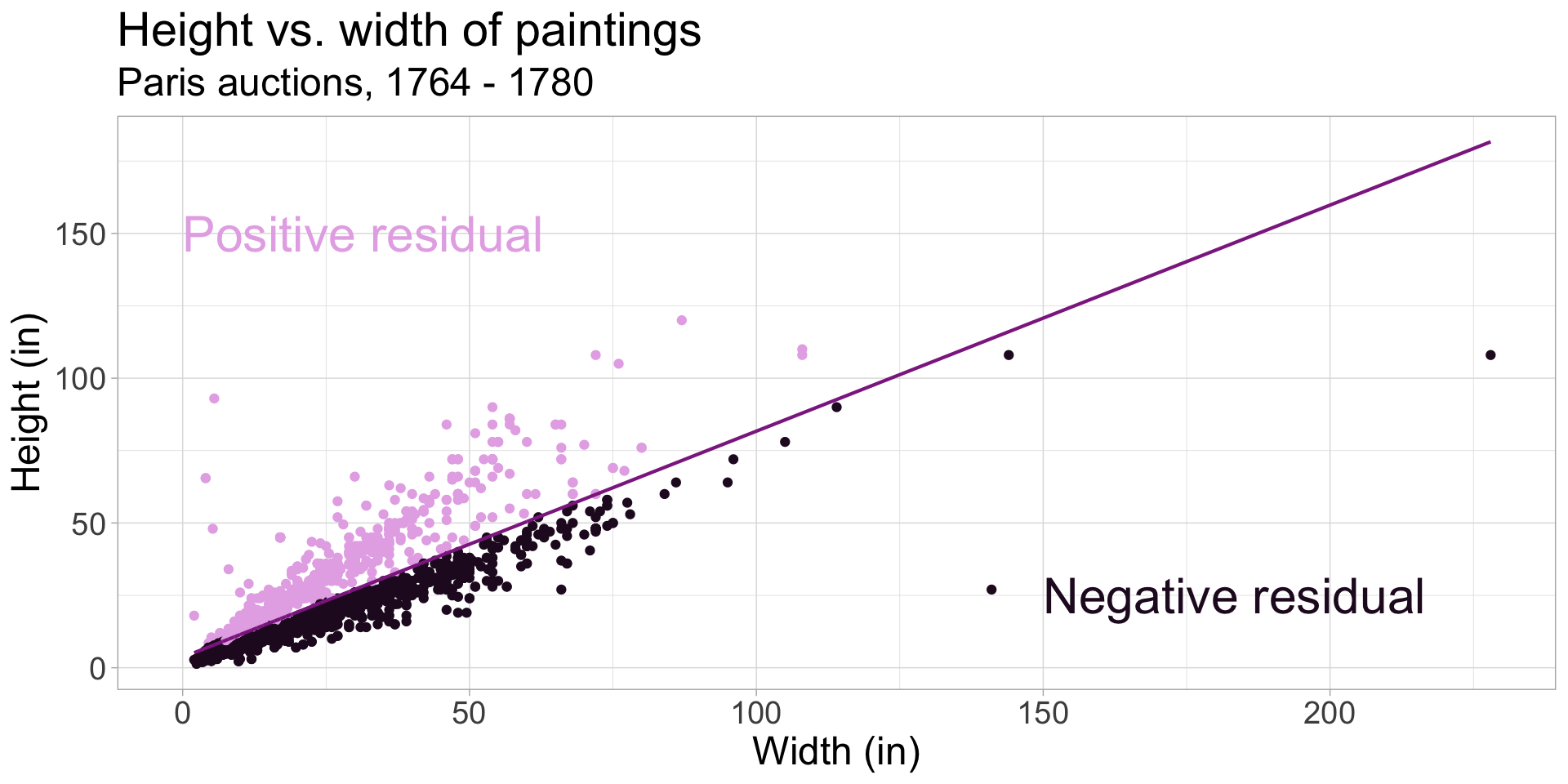
ht_wt_fit <- linear_reg() |>
  fit(height_in ~ width_in, data = pp)

ht_wt_fit_tidy <- tidy(ht_wt_fit$fit) 
ht_wt_fit_aug  <- augment(ht_wt_fit$fit) |>
  mutate(res_cat = ifelse(.resid > 0, TRUE, FALSE))

ggplot(data = ht_wt_fit_aug) +
  geom_point(aes(x = width_in, y = height_in, color = res_cat)) +
  geom_line(aes(x = width_in, y = .fitted), size = 0.75, color = "#8E2C90") + 
  labs(
    title = "Height vs. width of paintings",
    subtitle = "Paris auctions, 1764 - 1780",
    x = "Width (in)",
    y = "Height (in)"
  ) +
  guides(color = FALSE) +
  scale_color_manual(values = c("#260b27", "#e6b0e7")) +
  annotate("text", x = 0, y = 150, label = "Positive residual", color = "#e6b0e7", hjust = 0, size = 8) +
  annotate("text", x = 150, y = 25, label = "Negative residual", color = "#260b27", hjust = 0, size = 8)

Question

The plot below displays the relationship between height and width of paintings. The only difference from the previous plots is that it uses a smaller alpha value. What feature is apparent now that was not (as) obvious in the previous plots? What might be the reason for this feature?

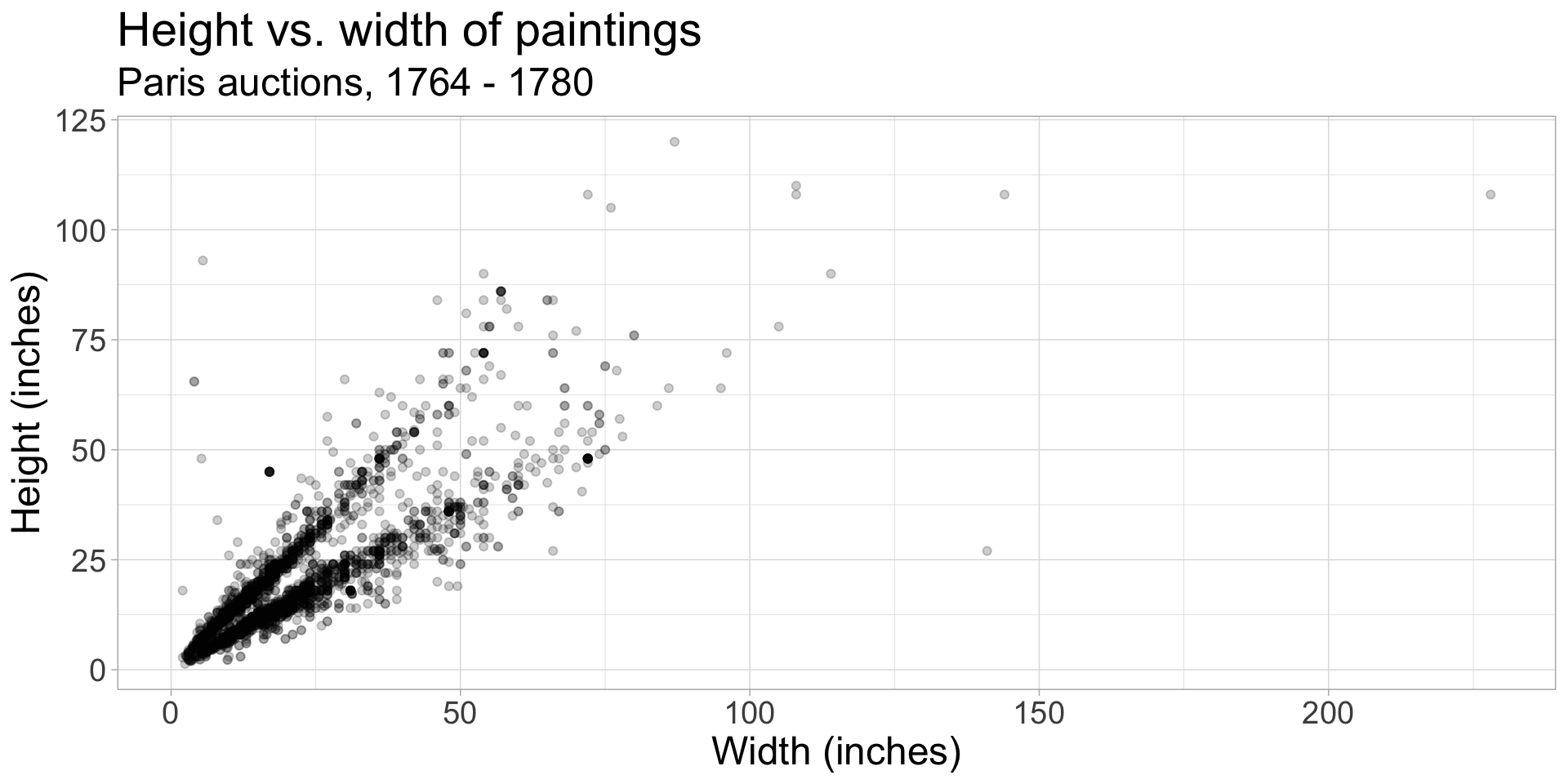
Landscape paintings vs. portraits

  • Landscape painting is the depiction in art of landscapes – natural scenery such as mountains, valleys, trees, rivers, and forests, especially where the main subject is a wide view – with its elements arranged into a coherent composition.1

  • Landscape paintings tend to be wider than they are long.

  • Portrait painting is a genre in painting, where the intent is to depict a human subject.2

  • Portrait paintings tend to be longer than they are wide.

Multiple explanatory variables

How would you expect the relationship between painting width and height to vary depending on whether or not a painting has any landscape elements?

ggplot(data = pp, aes(x = width_in, y = height_in, color = factor(lands_all))) +
  geom_point(alpha = 0.4) +
  geom_smooth(method = "lm", se = FALSE,
              fullrange = TRUE) +
  labs(
    title = "Height vs. width of paintings, by landscape features",
    subtitle = "Paris auctions, 1764 - 1780",
    x = "Width (inches)",
    y = "Height (inches)",
    color = "Landscape"
  ) +
  scale_color_manual(values = c("#E48957", "#071381"))

FYI you can extend regression lines

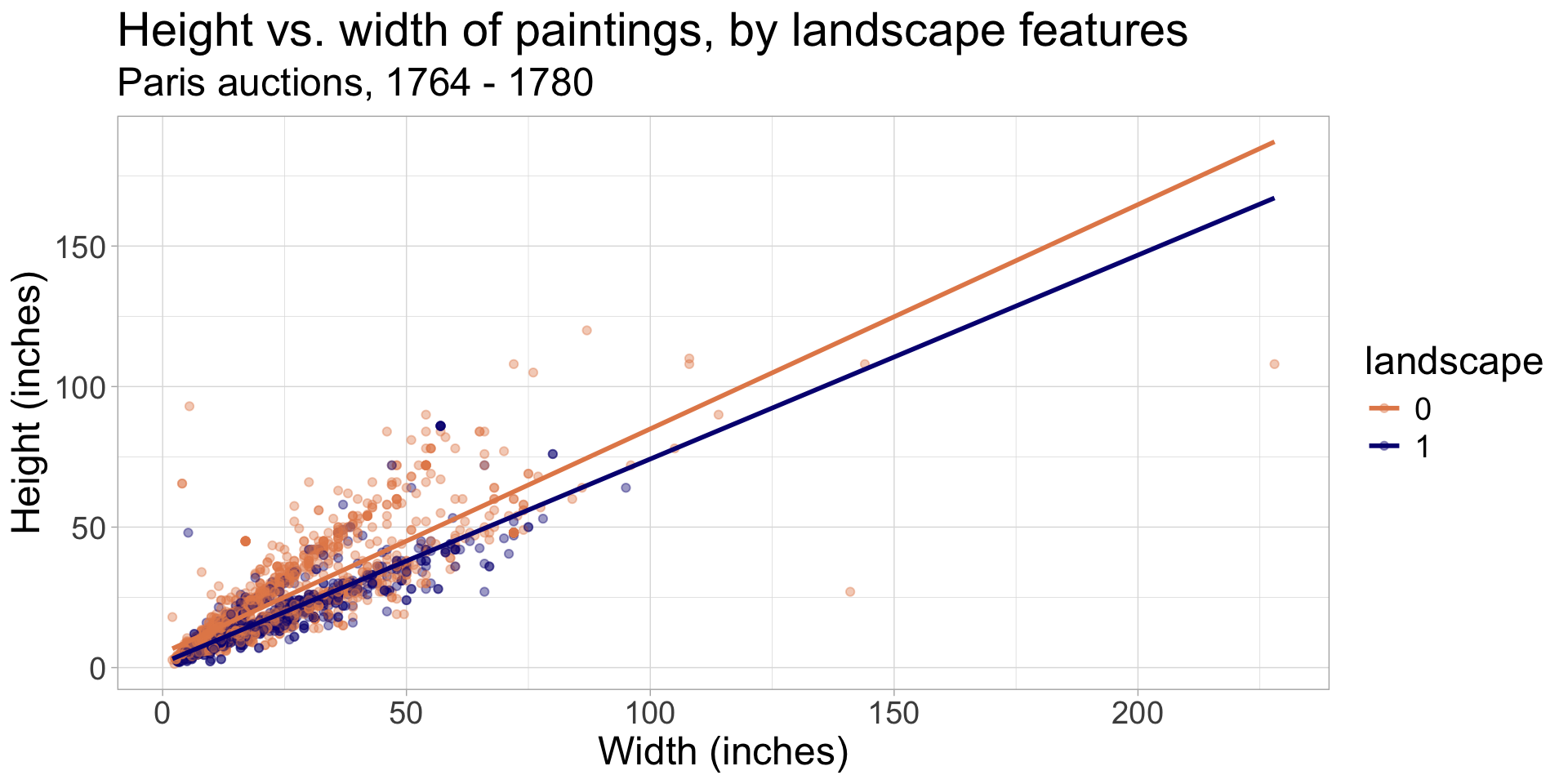
ggplot(data = pp, aes(x = width_in, y = height_in, color = factor(lands_all))) +
  geom_point(alpha = 0.4) +
  geom_smooth(method = "lm", se = FALSE,
              fullrange = TRUE) +
  labs(
    title = "Height vs. width of paintings, by landscape features",
    subtitle = "Paris auctions, 1764 - 1780",
    x = "Width (inches)",
    y = "Height (inches)",
    color = "landscape"
  ) +
  scale_color_manual(values = c("#E48957", "#071381"))

Models - upsides and downsides

  • Models can sometimes reveal patterns that are not evident in a graph of the data. This is a great advantage of modeling over simple visual inspection of data.

  • There is a real risk, however, that a model is imposing structure that is not really there on the scatter of data, just as people imagine animal shapes in the stars. A skeptical approach is always warranted.

Variation around the model…

is just as important as the model, if not more!

Statistics is the explanation of variation in the context of what remains unexplained.

  • The scatter suggests that there might be other factors that account for large parts of painting-to-painting variability, or perhaps just that randomness plays a big role.

  • Adding more explanatory variables to a model can sometimes usefully reduce the size of the scatter around the model. (We’ll talk more about this later.)

How do we use models?

  • Explanation: Characterize the relationship between \(y\) and \(x\) via slopes for numerical explanatory variables or differences for categorical explanatory variables

  • Prediction: Plug in \(x\), get the predicted \(y\)

Slopes vs. differences

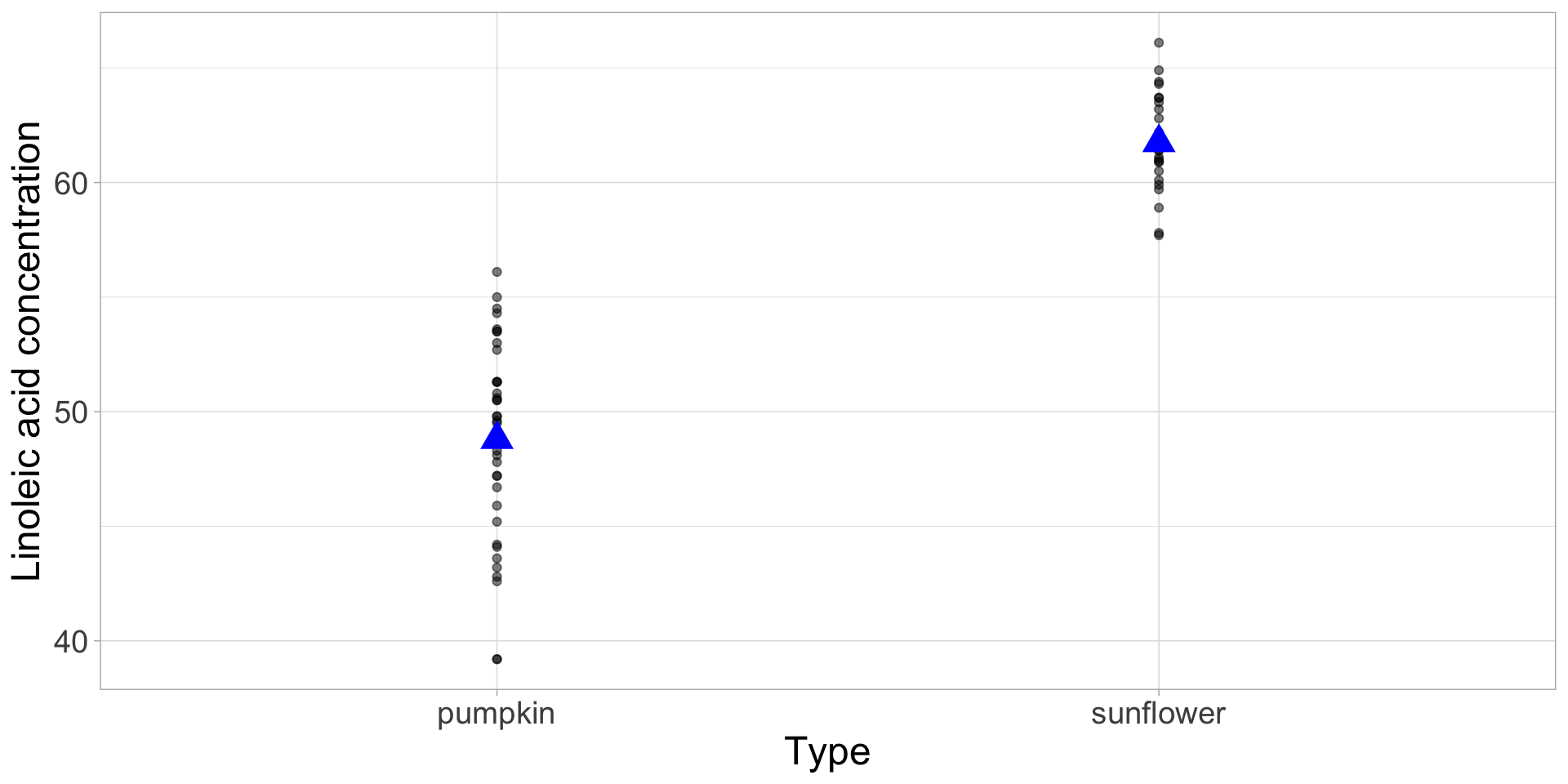
Slope: Two numeric variables; for every unit change in x, y changes by … units (the slope gives us …)

Slopes vs. differences

Difference: 1 numeric, 1 categorical variable; level a of the categorical variable (e.g., pumpkin) is, on average, … units higher/lower than level b of the categorical variable (e.g., sunflower)